好辣鸡啊……第一题推了一个小时后后期瞬间爆炸……太久不敲代码了已经成了咸鱼干…… 今天补了一下题,在这里记录一下。 Problem A. Square Counting
Problem
Mr. Panda has recently fallen in love with a new game called Square Off, in which players compete to find as many different squares as possible on an evenly spaced rectangular grid of dots. To find a square, a player must identify four dots that form the vertices of a square. Each side of the square must have the same length, of course, but it does not matter what that length is, and the square does not necessarily need to be aligned with the axes of the grid. The player earns one point for every different square found in this way. Two squares are different if and only if their sets of four dots are different. Mr. Panda has just been given a grid with R rows and C columns of dots. How many different squares can he find in this grid? Since the number might be very large, please output the answer modulo 109 + 7 (1000000007).
Input
The first line of the input gives the number of test cases, T. T lines follow. Each line has two integers R and C: the number of dots in each row and column of the grid, respectively.
Output
For each test case, output one line containing
Case #x: y, where x is the test case number
(starting from 1) and y is the number of different squares
can be found in the grid.
Limits
1 ≤ T ≤ 100.
Small dataset
2 ≤ R ≤ 1000. 2 ≤ C ≤ 1000.
Large dataset
2 ≤ R ≤ 109. 2 ≤ C ≤ 109.
Sample
Input
Output
4 2 4 3 4 4 4 1000 500
Case #1: 3 Case #2: 10 Case #3: 20 Case #4: 624937395
The pictures below illustrate the grids from the three sample cases
and a valid square in the third sample case. 


题目大意: 给出一个$ n m\(的正方形点阵,也就是\) (n-1) (m-1) $的棋盘,问存在多少个格点正方形(注意如最后一个图的倾斜的正方形也要计算)
做法: 默默推公式……一开始没注意倾斜的正方形导致方向错了好久,之后推导的过程还算顺利……叭(哭)
推导过程: 首先,我们考虑$ i i\(的方阵中存在多少能够“充满”整个方阵的格点多边形,“充满”意味着不会存在某一行或者某一列的方格与正方形没有相交的部分,我们先看\) i = 5$的情况:
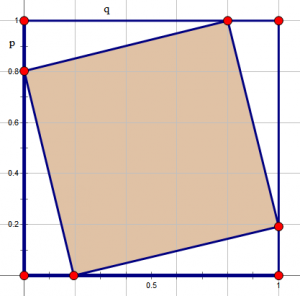
为了方便我们考虑所有的情况,上图举了个倾斜的例子。 对于边长是\(i\)的方阵,我们有\(p + q = i\),因此我们只需要统计方程\(p + q = i\)有多少非负整数解,显然有\(i+1\)种,但是\(\begin{cases} p=i \\ q=0
\end{cases}\)和\(\begin{cases} p=0 \\
q=i \end{cases}\)是同一种,因此总共有\(i\)种情况,而\(n\)行存在\(n-i+1\)个长度为\(i\)的方阵,\(m\)列存在\(m-i+1\)个长度为\(i\)的方阵,乘起来求和最终结果是: \[ \sum _{ i=1 }^{ min(n,m) }{ i\times
(n-i+1)\times (m-i+1) } \]
这样的结果求小数据是没问题了,大数据还是会TLE,我们需要求出求和公式。
求和公式的求法就不在这儿详述了,懒的话直接用WolframAlpha求也行。
最后公式是:(假设 \(m<{n}\)) \[\frac { (2n-m+1)\cdot (m+1)\cdot (m+2)\cdot m }{
12 }\] 取模过程的分母12的话逆元也好直接除也好,自行处理都不难:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
using namespace std;
const LL MOD=1000000007;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
if(a==0&&b==0) return -1;
if(!b){
x=1;y=0;
return a;
}
LL ans=exgcd(b,a%b,y,x);
y-=x*(a/b);
return ans;
}
LL inv(LL a,LL mod)
{
LL x,y;
LL d=exgcd(a,mod,x,y);
if(d==1) return (x+mod)%mod;
else return -1;
}
int main()
{
int T;
LL N,M;
scanf("%d",&T);
LL inv12=inv(12,MOD);
for(int cas=1;cas<=T;cas++){
scanf("%lld%lld",&N,&M);
N--,M--;
if(N<M) swap(N,M);
LL ans=(2*N+1-M)%MOD*(M+1)%MOD*(M+2)%MOD*M%MOD*inv12%MOD;
(ans+=MOD)%=MOD;
printf("Case #%d: %lld\n",cas,ans);
}
return 0;
}
Problem
Alice likes reading and buys a lot of books. She stores her books in
two boxes; each box is labeled with a pattern that matches the titles of
all of the books stored in that box. A pattern consists of only
uppercase/lowercase English alphabet letters and stars (*).
A star can match between zero and four letters. For example, books with
the titles GoneGirl and GoneTomorrow can be
put in a box with the pattern Gone**, but books with the
titles TheGoneGirl, and GoneWithTheWind
cannot. Alice is wondering whether there is any book that could be
stored in either of the boxes. That is, she wonders if there is a title
that matches both boxes' patterns.
Input
The first line of the input gives the number of test cases,
T. T test cases follow. Each consists
of two lines; each line has one string in which each character is either
an uppercase/lowercase English letter or *.
Output
For each test case, output one line containing
Case #x: y, where x is the test case number
(starting from 1) and y is TRUE if there is a
string that matches both patterns, or FALSE if not.
Limits
1 ≤ T ≤ 50.
Small dataset
1 ≤ the length of each pattern ≤ 200. Each pattern contains at most 5 stars.
Large dataset
1 ≤ the length of each pattern ≤ 2000.
Sample
Input
Output
3 **** It Shakese Sspeare Shakese peare Case #1: TRUE Case #2: TRUE Case #3: FALSE
题目大意: 给了两个模式串,类似通配符的方式,*能代表任意0~4个字符,问是否存在一个字符串能同时匹配这两个模式串。
做法: 啊竟然是dp,首先把每个*扩展成4个,然后用一个dp转移方程xjb转移就行,复杂度是\(O({ n }^{ 2 })\)的,讲道理最坏情况是\(8000 \times 8000\),但是大数据跑了6s也是能得到结果……讲道理大数据的实现是8min呢…… 转移的过程如下:用\(dp\[i\]\[j\]\)表示\(s\)串匹配到\(i\),\(p\)串匹配到\(j\)能否成功匹配:
\[if\quad dp[i][j]\quad then\\ \quad \quad \quad \quad \begin{cases} dp[i+1][j]|=s[i+1]=='*' \\ dp[i][j+1]|=p[j+1]=='*' \\ dp[i+1][j+1]|=s[i+1]=='*'||p[j+1]=='*'||s[i+1]==p[j+1] \end{cases}\]
简单解释下转移方程,首先,如果\(s\)的第\(i+1\)位是'*',那么可以从前一位\(\[i\]\[j\]\)的状态转移过来,\(p\)同理,另外,如果\(s\[i+1\]==p\[j+1\]\),状态也是可以可达的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
using namespace std;
char s[MAXN],p[MAXN],t[MAXN];
bool f[MAXN][MAXN];
int main(){
int T,len,ls,lp;
scanf("%d",&T);
for(int cas=1;cas<=T;cas++){
scanf("%s",t);
len=strlen(t);
ls=lp=0;
for(int i=0;i<len;i++)
if(t[i]=='*')
for(int k=4;k;k--) s[++ls]=0;
else s[++ls]=t[i];
scanf("%s",t);
len=strlen(t);
for(int i=0;i<len;i++)
if(t[i]=='*')
for(int k=4;k;k--) p[++lp]=0;
else p[++lp]=t[i];
for(int i=0;i<=ls;i++)
for(int j=0;j<=lp;j++)
f[i][j]=0;
f[0][0]=1;
for(int i=0;i<=ls;i++)
for(int j=0;j<=lp;j++)
if(f[i][j]){
f[i+1][j]|=!s[i+1];
f[i][j+1]|=!p[j+1];
f[i+1][j+1]|=!s[i+1]||!p[j+1]||s[i+1]==p[j+1];
}
printf("Case #%d: ",cas);
puts(f[ls][lp]?"TRUE":"FALSE");
}
return 0;
}
Problem
"Look at the stars, look how they shine for you." - Coldplay, "Yellow" In a galaxy far, far away, there are many stars. Each one is a sphere with a certain position (in three-dimensional space) and radius. It is possible for stars to overlap each other. The stars are so incredibly beautiful to you that you want to capture them forever! You would like to build two cubes of the same integer edge length, and place them in space such that for each star, there is at least one cube that completely contains it. (It's not enough for a star to be completely contained by the union of the two cubes.) A star is completely contained by a cube if no point on the star is outside the cube; a point exactly on a cube face is still considered to be inside the cube. The cubes can be placed anywhere in space, but they must be placed with their edges parallel to the coordinate axes. It is acceptable for the cubes to overlap stars or each other. What is the minimum integer edge length that allows you to achieve this goal?
Input
The input starts with one line containing exactly one integer T, which is the number of test cases. T test cases follow. Each test case begins with a line containing an integer, N, representing the number of stars. This is followed by N lines. On the ith line, there are 4 space-separated integers, Xi, Yi, Ziand Ri, indicating the (X, Y, Z) coordinates of the center of the ith star, and the radius of the ith star.
Output
For each test case, output one line containing
Case #x: y, where x is the test case number
(starting from 1) and y is the minimum cube edge length
that solves the problem, as described above.
Limits
1 ≤ T ≤ 100. -108 ≤ Xi ≤ 108, for all i. -108 ≤ Yi ≤ 108, for all i. -108 ≤ Zi ≤ 108, for all i. 1 ≤ Ri ≤ 108, for all i.
Small dataset
1 ≤ N ≤ 16.
Large dataset
1 ≤ N ≤ 2000.
Sample
Input
Output
3 3 1 1 1 1 2 2 2 1 4 4 4 1 3 1 1 1 2 2 3 4 1 5 6 7 1 3 1 1 1 1 1 1 1 1 9 9 9 1
Case #1: 3 Case #2: 5 Case #3: 2
题目大意: 三维空间给\(n\)个球,用两个相同的cube包含所有的球,求cube的最小棱长。
做法: 首先求出来最小包围cube,然后枚举两个cube在最小包围cube的八个顶点的哪个位置,对于每种情况二分棱长。 (感谢qqq的思路……没想到会这么简单……)
1 |
|