最后一个实验要求做一个RayTracing的小东西，本实验采用了Cornell Box作为模型，实现了简单的tracer。主要从以下几个方面简单的介绍一下：

算法框架

算法伪代码如上，即对每个像素点随机选取光线方向，如果击中点的话对其进行render，并根据反射、折射等递归计算，没有击中点则返回背景颜色。

数学基础

在实验的过程中，调用glm后发现实际的速度并没有快很多，反而各种方法比较凌乱，因此自己实现了一个Vector的struct：

#pragma once
#include "Calc.h"
struct Vec {
	double x, y, z;          
	Vec(double x_ = 0, double y_ = 0, double z_ = 0) { 
		x = x_; y = y_; z = z_; 
	}
	Vec operator+(const Vec &b) const {
		return Vec(x + b.x, y + b.y, z + b.z); 
	}
	Vec operator-(const Vec &b) const {
		return Vec(x - b.x, y - b.y, z - b.z); 
	}
	Vec operator*(double b) const {
		return Vec(x*b, y*b, z*b); 
	}
	Vec mult(const Vec &b) const { 
		return Vec(x*b.x, y*b.y, z*b.z); 
	}
	Vec& norm() { 
		return *this = *this * (1 / Qsqrt(x*x + y*y + z*z)); 
	}
	double dot(const Vec &b) const {
		return x*b.x + y*b.y + z*b.z; 
	} 
	Vec cross(const Vec &rhs) {
		return Vec(y * rhs.z - z * rhs.y,
			z * rhs.x - x * rhs.z,
			x * rhs.y - y * rhs.x);
	}
};

这里面有个叫做Qsqrt的东西，其实是鼎鼎有名的卡马克常数的那个平方根快速算法，具体解释我可能有时间再写一篇博客探讨下：

#pragma once
float Qsqrt(float number)//By Carmark
{
	int i;
	float x2, y;
	const float threehalfs = 1.5F;
	x2 = number * 0.5F;
	y = number;
	i = *(int *)&y;
	i = 0x5f375a86 - (i >> 1);
	y = *(float *)&i;
	y = y * (threehalfs - (x2 * y * y));
	y = y * (threehalfs - (x2 * y * y));
	y = y * (threehalfs - (x2 * y * y));
	return number*y;
}

光线

光线类，o和d分别表示起始位置和方向

1
2
3

#pragma once
#include "Vecter.h"
struct Ray { Vec o, d; Ray(Vec o_, Vec d_) : o(o_), d(d_) {} };

球

之后写了一个叫做Sphere的类，材质包括漫反射、反射与折射，并实现一下与光线相交的函数，返回光线的参数方程（o+td）中第一个交点的t：

#pragma once
#include "Ray.h"
#include "Calc.h"
enum Refl_t { DIFF, SPEC, REFR };
struct Sphere {
	double rad;       
	Vec p, e, c;	// position, emission, color;
	Refl_t refl;
	Sphere(double rad_, Vec p_, Vec e_, Vec c_, Refl_t refl_) :
		rad(rad_), p(p_), e(e_), c(c_), refl(refl_) {}
	double intersect(const Ray &r) const { // returns distance, 0 if nohit 
		Vec op = p - r.o; 
		double t, eps = 1e-4, b = op.dot(r.d), det = b*b - op.dot(op) + rad*rad;
		if (det<0) 
			return 0; 
		else 
			det = Qsqrt(det);
		return (t = b - det)>eps ? t : ((t = b + det)>eps ? t : 0);
	}
};

场景构建

由于当半径很大的时候，球的部分表面可以被看做是平面，因此不必单独写平面的类，直接调用sphere就好。下面的代码设置了上下左右前后六个表面、灯光和材质分别是反射和折射的两个球：

Sphere spheres[] = {//Scene: radius, position, emission, color, material 
	Sphere(1e5, Vec(1e5 + 1,40.8,81.6), Vec(),Vec(.75,.25,.25),DIFF),//Left 
	Sphere(1e5, Vec(-1e5 + 99,40.8,81.6),Vec(),Vec(.25,.25,.75),DIFF),//Rght 
	Sphere(1e5, Vec(50,40.8, 1e5),     Vec(),Vec(.75,.75,.75),DIFF),//Back 
	Sphere(1e5, Vec(50,40.8,-1e5 + 170), Vec(),Vec(),           DIFF),//Frnt 
	Sphere(1e5, Vec(50, 1e5, 81.6),    Vec(),Vec(.75,.75,.75),DIFF),//Botm 
	Sphere(1e5, Vec(50,-1e5 + 81.6,81.6),Vec(),Vec(.75,.75,.75),DIFF),//Top 
	Sphere(16.5,Vec(27,16.5,47),       Vec(),Vec(1,1,1)*.999, SPEC),//Mirr 
	Sphere(16.5,Vec(73,16.5,78),       Vec(),Vec(1,1,1)*.999, REFR),//Glas 
	Sphere(600, Vec(50,681.6 - .27,81.6),Vec(12,12,12),  Vec(), DIFF) //Lite 
};

图像、采样率、摄像机的设置

设置一些基本的图像参数，用于进一步的构建图像：

1
2
3

int w = 1024, h = 768, samps = 1; 
Ray cam(Vec(50, 52, 295.6), Vec(0, -0.042612, -1).norm()); // camera position direction
Vec cx = Vec(w*.5135 / h), cy = (cx.cross(cam.d)).norm()*.5135, r, *c = new Vec[w*h];

循环处理像素点

对于每个像素点，选取它的四邻域进行随机取样，取样的个数就是采样率的samps：

for (int y = 0; y&lt;h; y++) {                       // Rows
	fprintf(stderr, "\rRendering (%d spp) %5.2f%%", samps * 4, 100.*y / (h - 1));
	for (unsigned short x = 0; x&lt;w; x++)   // Cols 
		for (int sy = 0, i = (h - y - 1)*w + x; sy&lt;2; sy++)     
			for (int sx = 0; sx&lt;2; sx++, r = Vec()) {        // 2x2 subpixel cols 
				for (int s = 0; s&lt;samps; s++) {	//samples
					double r1 = 2 * random(), dx = r1&lt;1 ? sqrt(r1) - 1 : 1 - sqrt(2 - r1);
					double r2 = 2 * random(), dy = r2&lt;1 ? sqrt(r2) - 1 : 1 - sqrt(2 - r2);
					Vec d = cx*(((sx + .5 + dx) / 2 + x) / w - .5) + cy*(((sy + .5 + dy) / 2 + y) / h - .5) + cam.d;
					r = r + radiance(Ray(cam.o + d * 140, d.norm()), 0)*(1. / samps);
				} 
				c[i] = c[i] + Vec(clamp(r.x), clamp(r.y), clamp(r.z))*.25;
			}

其中，radiance就是进行raycast的递归过程，计算之后对各个采样点计算得来的颜色取平均值。

RayCast过程

即radiance过程，是一个递归的过程，首先intersect方法得到这个光线击中的物体：

inline bool intersect(const Ray &r, double &t, int &id) {
	double n = sizeof(spheres) / sizeof(Sphere), d, inf = t = 1e20;
	for (int i = int(n); i--;) 
		if ((d = spheres[i].intersect(r)) && d<t) {
			t = d; id = i; 
		}
	return t<inf;
}

设置了递归的深度是5，得到击中的物体后计算法向量（和背面剔除后的法向量），如果递归超过深度则按照概率衰减或直接返回强度（灯光）

double t;                               
int id = 0;                               
if (!intersect(r, t, id)) 
	return Vec();  
const Sphere &obj = spheres[id];        
Vec x = r.o + r.d*t, n = (x - obj.p).norm(), nl = n.dot(r.d)<0 ? n : n*-1, f = obj.c;//n:normal nl:backface culling normal
double p = f.x>f.y && f.x>f.z ? f.x : f.y>f.z ? f.y : f.z; // p:max refl
if (++depth>5) 
	if (random()<p) 
		f = f*(1 / p); 
	else 
		return obj.e;

之后是漫反射、镜面反射的着色过程，在之前的博客中有提及，这里不再赘述计算过程。需要注意的是，漫反射之后的来源光线是随机选取的，随机的过程可以用下图表示。

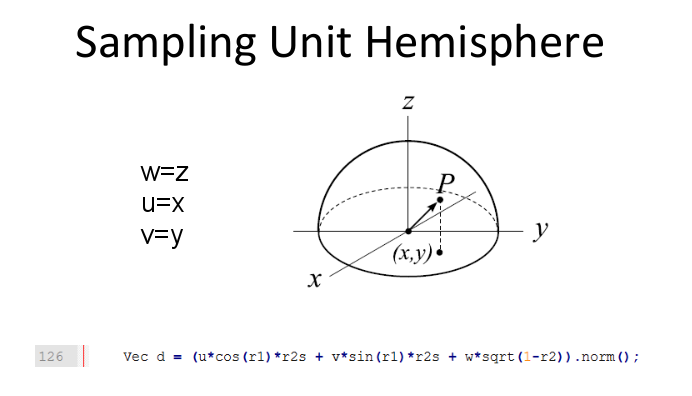
if (obj.refl == DIFF) { 
	double r1 = 2 * M_PI*random(), r2 = random(), r2s = sqrt(r2);
	Vec w = nl, u = ((fabs(w.x)>.1 ? Vec(0, 1) : Vec(1)).cross(w)).norm(), v = w.cross(u);
	Vec d = (u*cos(r1)*r2s + v*sin(r1)*r2s + w*sqrt(1 - r2)).norm();
	return obj.e + f.mult(radiance(Ray(x, d), depth));
}
else if (obj.refl == SPEC)
	return obj.e + f.mult(radiance(Ray(x, r.d - n * 2 * n.dot(r.d)), depth))

之后是折射与反射的判断关系……首先要复习一下全反射（Total internal reflection ）的相关知识，判断一下是需要进行全反射就好还是需要进一步计算折射：

如果有折射，用下面这张图中的公式计算：

Ray reflRay(x, r.d - n * 2 * n.dot(r.d));     // Ideal dielectric REFRACTION 
bool into = n.dot(nl)>0;                // Ray from outside going in? 
double nc = 1, nt = 1.5, nnt = into ? nc / nt : nt / nc, ddn = r.d.dot(nl), cos2t;
if ((cos2t = 1 - nnt*nnt*(1 - ddn*ddn))<0)    // Total internal reflection 
	return obj.e + f.mult(radiance(reflRay, depth));
Vec tdir = (r.d*nnt - n*((into ? 1 : -1)*(ddn*nnt + sqrt(cos2t)))).norm();
double a = nt - nc, b = nt + nc, R0 = a*a / (b*b), c = 1 - (into ? -ddn : tdir.dot(n));
double Re = R0 + (1 - R0)*c*c*c*c*c, Tr = 1 - Re, P = .25 + .5*Re, RP = Re / P, TP = Tr / (1 - P);
return obj.e + f.mult(depth>2 ? (random()<P ?   // Russian roulette 
	radiance(reflRay, depth)*RP : radiance(Ray(x, tdir), depth)*TP) :
	radiance(reflRay, depth)*Re + radiance(Ray(x, tdir), depth)*Tr);

最后结果

输出ppm图像如下：

FILE *f;
	errno_t err;
	err = fopen_s(&f, "image.ppm", "w"); 
	fprintf(f, "P3\n%d %d\n%d\n", w, h, 255);
	for (int i = 0; i<w*h; i++)
		fprintf(f, "%d %d %d ", toInt(c[i].x), toInt(c[i].y), toInt(c[i].z));

采样率低的时候噪点很多，随着采样率升高效果逐渐平滑和稳定：

Bluefissure's Blog

Computer Graphics Final Project Simple RayTracing